前回の記事giveme5.hateblo.jp
において,「tの増大とともにΔw(t)とΔw(x,y)の近似は悪くなる傾向にあるようである」と述べたが, 前回はtの増大の結果, Δw(t)とΔw(x,y)の値が計算不能となったため, 最終的な結論は出せないままであった. 今回はこの点について検証してみる.
まず変数x, yの定義を次のように変更する.
x=exp(t+1)
y=sin t +1
その目的は, 変数の増大を抑制するためである.
w=x^y
と定義されるwは少なくともt<1.57の範囲で単調増加するが, その増加は変数x,yについては, それぞれx<14, y<2に抑制され, その結果wの増加もw<171に抑制される. こうして前回のように計算不能となることはない.
Δw(x,y)=y{x^(y-1)}Δx+{(x^y) logx}Δy
Δw(t)=(x+Δx)^(y+Δy)-x^y
のそれぞれの値をエクセルで計算した結果は, 以下のとおりである. なお計算においてはΔt=0.00001と固定し(そのときΔxは単調増加するが, Δyは単調減少する)変数tの値を0.1から1.57まで変化させた.
なおR=Δw(t)/Δw(x,y), r=(R-1)×100000000である.
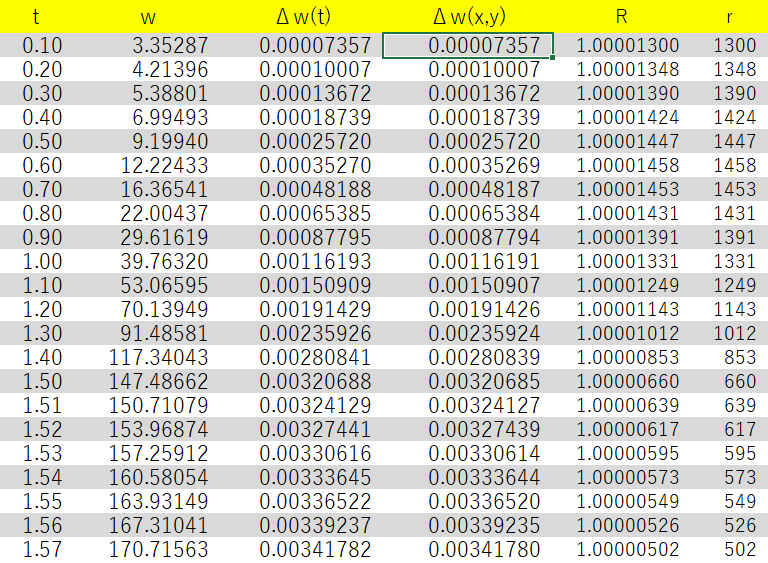
Δw(t)とΔw(x,y)は, ともにtの増加に伴って単調に増加する. そしてt=0.6まではrは単調に増加する(Δw(t)とΔw(x,y)の差は拡大する)が, t=0.7以降は, rは逆に単調減少に転じる(Δw(t)とΔw(x,y)の差は縮小する).
したがって今回の検証から, 一概に「tの増大とともにΔw(t)とΔw(x,y)の近似は悪くなる傾向にある」とは言えないという結論が導き出される.